When Affinity Propagation Clustering outperforms Kmeans ?
Affinity propagation is an unsupervised clustering algorithm used when number of optimal clusters are unknown
Affinity Propagation is a clustering technique based on the concept of “message passing” between data points.
The algorithm creates clusters by sending messages between data points until convergence. It takes as input the similarities between the data points and identifies exemplars based on certain criteria. Messages are exchanged between the data points until a high-quality set of exemplars are obtained.
Unlike clustering algorithms such as k-means or k-medoids, affinity propagation does not require the number of clusters to be determined or estimated before running the algorithm.
Lets have a deeper dig into the topic.
Dataset
Let us consider the following dataset in order to understand the working of the Algorithm.
Similarity Matrix
Every cell in the similarity matrix is calculated by negating the sum of the squares of the differences between participants.
For example, the similarity between Alice and Bob, the sum of the squares of the differences is (3–4)² + (4–3)² + (3–5)² + (2–1)² + (1–1)² = 7. Thus, the similarity value of Alice and Bob is -(7).
The algorithm will converge around a small number of clusters if a smaller value is chosen for the diagonal, and vice versa. Therefore, we fill in the diagonal elements of the similarity matrix with -22, the lowest number from among the different cells.
Responsibility Matrix
We will start by constructing an availability matrix with all elements set to zero. Then, we will be calculating every cell in the responsibility matrix using the following formula:
Here i refers to the row and k refers to the column of the associated matrix.
For example, the responsibility of Bob (column) to Alice (row) is -1, which is calculated by subtracting the maximum of the similarities of Alice’s row except similarity of Bob to Alice (-6) from similarity of Bob to Alice(-7).
After calculating the responsibilities for the rest of the pairs of participants, we end up with the following matrix.
Availability Matrix
In order to construct an Availability Matrix we will be using two separate equations for on diagonal and off diagonal elements and will be applying them on our responsibility matrix.
For the Diagonal elements the below mentioned formula will be used.
Here i refers to the row and k the column of the associated matrix.
In essence, the equation is telling us to calculate the sum all the values above 0 along the column except for the row whose value is equal to the column in question. For example, the on diagonal elemental value of Alice will be the sum of the positive values of Alice’s column excluding Alice’s self-value which will be then equal to 21(10 + 11 + 0 + 0).
After Partial Modification our Availability Matrix would look like this:
Now for the off diagonal elements the following equation will be used to update their values.
Lets try to understand the above equation with a help of an example. Suppose we need to find the availability of Bob (column) to Alice (row) then it would be the summation of Bob’s self-responsibility(on diagonal values) and the sum of the remaining positive responsibilities of Bob’s column excluding the responsibility of Bob to Alice (-15 + 0 + 0 + 0 = -15).
After calculating the rest, we wind up with the following availability matrix.
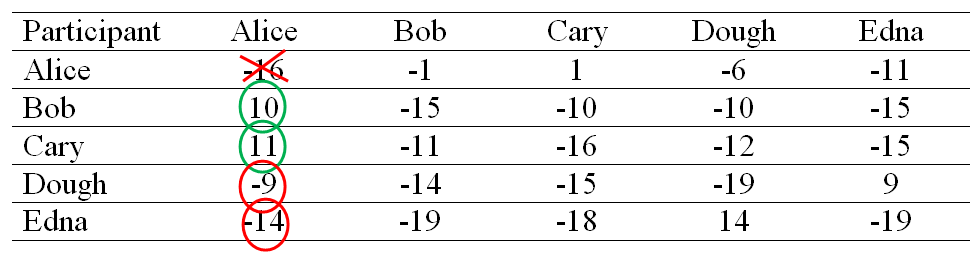
Criterion Matrix
Each cell in the criterion matrix is simply the sum of the availability matrix and responsibility matrix at that location.
The column that has the highest criterion value of each row is designated as the exemplar. Rows that share the same exemplar are in the same cluster. Thus, in our example. Alice, Bob, Cary Doug and Edna all belongs to the same cluster.
If in case the situation might go somewhat like this:
then Alice, Bob, and Cary form one cluster whereas Doug and Edna constitute the second.
Code
Import the libraries
import numpy as np
from matplotlib import pyplot as plt
import seaborn as sns
sns.set()
from sklearn.datasets import make_blobs
from sklearn.cluster import AffinityPropagationGenerating Clustered Data From Sklearn
X, clusters = make_blobs(n_samples=1000, centers=5, cluster_std=0.8, random_state=0)
plt.scatter(X[:,0], X[:,1], alpha=0.7, edgecolors='b')Initialization and Fitting the model.
af = AffinityPropagation(preference=-50)
clustering = af.fit(X)Plotting the Data points
plt.scatter(X[:,0], X[:,1], c=clustering.labels_, cmap='rainbow', alpha=0.7, edgecolors='b')Conclusion
Affinity Propagation is an unsupervised machine learning technique that is particularly used where we don’t know the optimal number of clusters.
Credits
The above article is sponsored by Vevesta.
Vevesta: Your Machine Learning Team’s Collective Wiki: Identify and use relevant machine learning projects, features and techniques.
100 early birds who login to Vevesta get free subscription for 3 months
Subscribe to receive a copy of our newsletter directly delivered to your inbox.
References