Transformer Layers as Painters
Understanding how Transformer's layers actually function
I blog about latest machine learning research topics that have an immediate impact on the work us data scientists/machine learning engineers do every day. Share the newsletter with your friends so that we all grow together.
Abstract
The research paper talks about the middle layers in a transformer as painters. According to authors[1], “each painter uses the same ‘vocabulary’ for understanding paintings, so that a painter may receive the painting from a painter earlier in the assembly line without catastrophe.”
Deeper Dive into the paper
The authors use different execution strategies to conduct the study, as indicated in the Figure 1 and pretrained models were used in this study.
We step into multiple nuances brought out in the paper by answering the following questions:
Do layers use the same representation space?
The authors[1] investigate this by either skipping a layer or switching the order of middle layers. The study found that the transformer probably has three representations - lower, middle and topmost layers, that is each layers have their own understanding of the data representation space. More importantly, the authors found that the middle layers seem to share a common representation space.
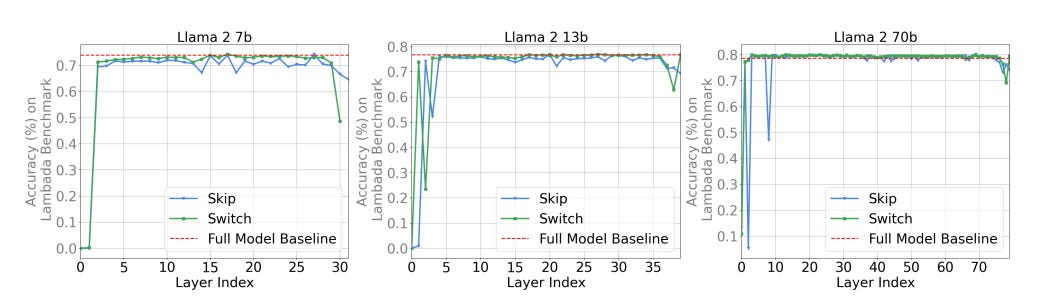
Are all the layers necessary?
They found that skipping few middle layers doesn’t not drastically impact the performance of the model as seen in Figure 2. It is also seen that fine tuning can improve the performance of the transformer, when few (not to many) layers are skipped.
Technique used:
The authors skip M-1 layers by sending the output from N layer to N + M layer.
Are middle layers all doing the same function?
The layers share the same representation space but the authors found that each middle layer perform a different function and sharing weights between middle layers can be catastrophic.
Does the layer order matter?
Answer to the question in the words of the authors - “Somewhat. Both randomizing and reversing the middle layer order has graceful degradation.”
According to authors, “The previous experiments suggest that middle layers share a representation space but perform different operations on this space. Another question is how much the order of these function matters ?”. The authors found that order of middle layers mattered somewhat.
Technique used:
To investigate this they used two techniques. One was to reverse the order of middle layers and the second was to randomize the order of middle layers. It was found that transformer performed worse when the order of middle layers were reversed as compared to randomization of the layers.
Can we run the layers in parallel?
It was found that the model performance showed gradual degradation for almost all of the benchmarks except GSM8K.
Technique used:
The layers N to T- M were run in parallel and then their results were averaged.
Does order matter for some tasks more than others?
Mathematical and reasoning tasks are more dependent on the order of middle layers than “semantic” tasks.
Technique used :
Refer to Figure 1, the techniques - reverse, skip and parallel were used to test for this question.
Does looping help parallelized layers?
Yes, looping helps parallelized layers and with, some exceptions, the optimal number of iterations over the loop are proportional to the number of parallelized layers.
Technique used:
Looping parallel as explained in figure 1 was used to test this.
Which variants harm performance the least?
Replacing a period of middle layers with exactly the same number of copies of the middlemost layer (called Middle Repeat) – does worst by far, quickly degrading to random baseline performance. On the other hand, looped-parallel and random layer order have the shallowest degradation.