The Zero Inflated Poisson Regression Model - How to model data with lot of zeroes?
Model count data that has an excess of zero counts
Zero-inflated Poisson regression is used to model count data that has an excess of zero counts. By this I mean that the dependent variable has large number zeros. The theory suggests that the excess zeros are generated by a separate process from the count values and that the excess zeros can be modeled independently. Thus, the zip model has two parts, a Poisson count model and the logit model for predicting excess zeros.
In this section, we’ll learn how to build a regression model for count based datasets in which the dependent variable contains an excess of zero-valued data.
Count based regression models are used where the value of dependent variable is a whole number. Few of the use cases of this model are:
Number of hits on the website per hour.
Number of life insurance claims filed per year.
Number of children a couple has.
Number of doctor visits per year.
In the real world scenario there are many cases that produce counts which are almost always zero. For example:
Number of planets discovered each year.
The number of millionaires living in every single city in the world.
Mathematics behind Zip Model
When the Poisson regression model is applied to the count outcome data in real world, it is not rare to see the poor model fit indicated by a deviance or Pearson’s chi-square.
The zero-inflated Poisson (ZIP) is an alternative that can be considered here. This model allows for assuming that there are two different types of individuals in the data: (1) Those who have a zero count with a probability of 1 (Always-0 group), and (2) those who have counts predicted by the standard Poisson (Not always-0 group). Observed zero could be from either group, and if the zero is from the Always-0 group, it indicates that the observation is free from the probability of having a positive outcome.
The overall model is a mixture of the probabilities from the two groups, which allows for both the over dispersion and excess zeros that cannot be predicted by the standard Poisson model.
Having a membership of Always-0 group is a binary outcome that can be predicted by logit model.
The probability (𝜓𝑖) that the observation 𝑖 is in Always-0 group is predicted by the characteristic of observation 𝑖, so that can be written as: 𝜓𝑖 = 𝐹(𝑧𝑖 ′𝛾) where 𝑧𝑖 is the vector of covariates and 𝛾 is the vector of coefficients of logit regression.
Then the probability that the observation 𝑖 is in Not always-0 group becomes (1-𝜓𝑖) . For observations in Not always-0 group, their positive count outcome is predicted by the standard Poisson model, so that can be written as:
where 𝜇𝑖 is the conditional mean.
Then, mixed probabilities for ZIP are expressed as follows:
Zero counts in Always-0 group
Zero counts in Not Always-0 group
Non zero counts in Not Always- group
Overall
Here is the practical use case of the same where the state wildlife biologists want to model how many fishes are being caught by the visitors visiting the state park. Some visitors do not fish, but there is no data on whether a person fished or not. Some visitors who did fish did not catch any fish so there are excess zeros in the data because of the people that did not fish.
How to train the ZIP model using Python?
In our Python tutorial on the ZIP model, we’ll use a data set of camping trips taken by 250 groups of people, the data looks something like this:
Here is a frequency of Dependent Variable i.e. Fish Count in the dataset,
As we can see, there are excess zeroes in this data set. We’ll train a ZIP model on this data set to test this theory and hopefully achieve a better fit than the regular Poisson model.
Regression Goal
Predict the number of fish caught (FISH_COUNT) by a camping group based on the values of LIVE_BAIT, CAMPER, PERSONS and CHILDREN variables.
Performing Train-Test Split
Fitting the ZIP model and Calculating RMSE
Here, endog is our dependent variable, exog is the dataset containing the features or the independent variables and inflation is the model for zero inflation which can be either logit or probit.
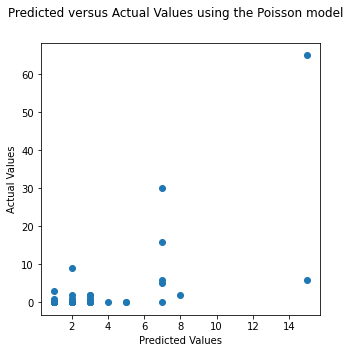
Plotting the Actual and Predicted Values
Comparing the results with Poisson Distribution
RMSE(ZIP Model) =7.937253933193772
RMSE(Poisson Regression)=8.37973746605465
It is clearly noticeable that the ZIP model has outperformed the Regular Poisson Model on these type of excess zero datasets.
Dumping the model in Excel Sheet using VevestaX
Brief Intro about VevestaX
VevestaX is an open source Python package which includes a variety of features that makes the work of a Data Scientist pretty much easier especially when it comes to analyses and getting the insights from the data.
The package can be used to extract the features from the datasets and can track all the variables used in code.
The best part of this package is about its output. The output file of the VevestaX provides us with numerous EDA tools like histograms, performance plots, correlation matrix and much more without writing the actual code for each of them separately.
How to Use VevestaX?
Install the package using:
pip install vevestaX
Import the library in your kernel as:
from vevestaX import vevesta as v
V=v.Experiment( )
To track the feature used:
V.ds = df
where df is the pandas data frame containing the features.
To track features engineered
V.fe = df
Finally in order to dump the features and variables used into an excel file and to see the insights what the data carries use:
V.dump(techniqueUsed=’ZIP Model’,filename=”ZIP.xlsx”,message=”Zero Inflated Poisson Model was used”,version=1)
To write the details to www.Vevesta.com:V.commit(techniqueUsed = “Zip Model”, message=”increased accuracy”, version=1, projectId=128, attachmentFlag=True)
Credits
The above article is sponsored by Vevesta.
Vevesta: Your Machine Learning Team’s Collective Wiki: Identify and use relevant machine learning projects, features and techniques
100 early birds who login to Vevesta get free subscription for 3 months.
Subscribe to our weekly newsletter to stay updated on latest machine learning/MLOps articles.
References: