Layman's Guide to Lottery Ticket Hypothesis In Neural Network
Finding lighter trainable subnetworks from fully-connected feed-forward networks with similar performance
Idea behind Lottery Ticket Hypothesis
Imagine we have a fully functioning car which only used by a single person but its too cost expensive and needs heavy maintenance so you trim and tinker it down and use the cores of the car to make a vehicle that carries the essence and materials of the car and by doing so is more lightweight, faster and therefore is more functionally efficient, which you couldn’t do before but by using a special technique you're able to accomplish this transformation that is the idea behind the lottery ticket hypothesis.
Definition Of Lottery Ticket Hypothesis
“A randomly initialized dense neural network contains a subnetwork that is initialized such that when trained in isolation it can match the test accuracy of the original network after training for at most the same number of iterations.”
Introduction to Lottery Ticket Hypothesis
The work by Frankle and Carbin (2018) has presented a surprising phenomenon: pruned neural networks can be trained to achieve performance as compared with the unpruned neural network when resetting their weights to their initial values.
It’s found that after the application these pruning techniques automatically uncover trainable subnetworks from fully-connected feed-forward networks. We call these trainable subnetworks, “winning tickets” since those that we find have won the initialization lottery with a combination of weights and connections capable of learning. These winning tickets when trained in isolation can reach test accuracy comparable to the original network in a similar number of iterations. However, what is observed is that the sparse architectures produced by pruning are quite tough to train from the start. to understand fully Lottery Ticket Hypothesis we must first know what is pruning and their types.
Saga of the Lottery Ticket Hypothesis
Pruning
In theory, the pruned subnetwork should perform similarly to the dense network, though this may not be the case if a large number of parameters or weights are removed. Thus, the goal of the pruning process is to find and remove parameters that do not significantly affect the performance of the network.
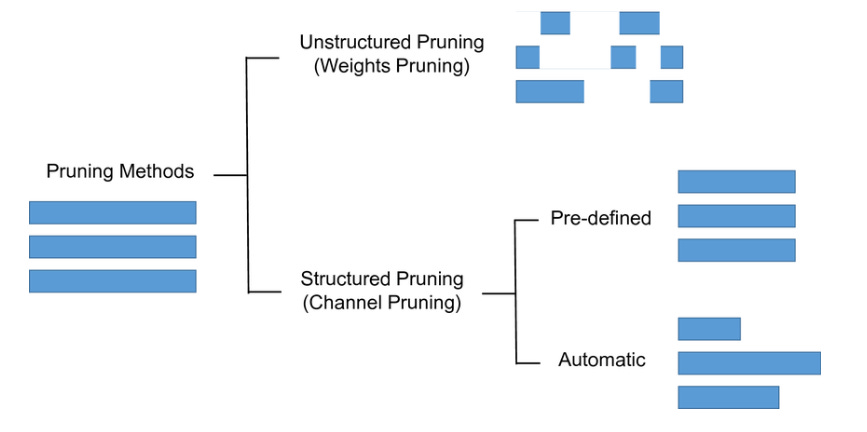
In total there are four types of pruning namely
Structured and Unstructured,
Scoring,
Iterative and fine-tuning,
Scheduling.
In the lottery ticket hypothesis, we’ll only be needing structured, unstructured, and iterative pruning so we must take a deeper look into them.
Types of pruning
Structured and Unstructured Pruning:
A Beginners Guide to Neural Network Pruning
In the Unstructured pruning approach, there are no limitations to how one wants to prune the neural network. The liberty to alter each or all weights and can remove them completely, making the pruning process more experimental. Since only the weights are varied in the neural network this process is also called Weight Pruning. This results in a sparse neural network. On the contrary, in the structured pruning method entire group of weight, or as we call it neurons in a feed-forward network is removed altogether. This is also known as Unit/Neuron Pruning and the resultant is a dense neural network.
Both the methods are widely applied in neural networks and each comes with a trade of its own but arguably unstructured pruning is considered to be preferable since it places no restrictions on the order of pruning.
Iterative Pruning:
Saga of the Lottery Ticket Hypothesis
Some methods prune the desired amount all at once, which is often referred to as One-shot Pruning. The network is trained all at once and bulk p% of the weights are pruned off of the network. certain systems, known as Iterative Pruning, repeat the process of pruning the network to some extent and retraining it until the desired pruning rate is obtained so for each round it prunes p^1/n% of the parameters, trains, and reprunes repeating this n times. It's used for approaches that require fine-tuning, it is most typical to continue training the network with the weights that were trained before pruning. Another method could be re-initializing the network with the same resultant weights. Now that we have understood the basic idea about pruning let's look at the theory behind the Lottery ticket hypothesis.
Limitations of Pruning and How Lottery Ticket Hypothesis Overcame The Barrier-
Originally pruning is a common practice, it has been used to decrease the storage size of networks, and decrease the energy consumption and the inference time but the problem which arose was that these pruned weight networks couldn't be trained from scratch or with random parameters. Hence once pruned the network could only be fine-tuned with no chance of experimentation as the network couldn't be trained from scratch but that was the limitation that was overcome by the lucky ticket hypothesis.
The initialization is the key to training these pruned networks from scratch. Once the winning ticket which is our subnetwork with peak required conditions is found the same initialization parameters are maintained. In this way, the winning ticket; both its structure and its weights; exists within the randomly-initialized dense network. Thus, this subnetwork is shown to have won the “initialization lottery”, as it can be trained from scratch to higher accuracy than that of a fully-trained dense network or randomly re-initialized subnetwork with the same structure. Their connections have initial weights that make training particularly effective.
Let’s suppose we have with us a neural network with its own initial parameters and after training all the way to convergence it will have a different set of weight and parameters. Now we prune the neural network to find the winning ticket. Once the winning ticket is found to retrain this subnetwork we’ll have to reinitialize this pruned network with the same parameter the network had when it started out. By this we ensure that we have the same structure and initial weights helping us to retrain from scratch and reach better accuracy as the outcome. These lottery tickets tend to be 10% to 20% of the original size of the network.
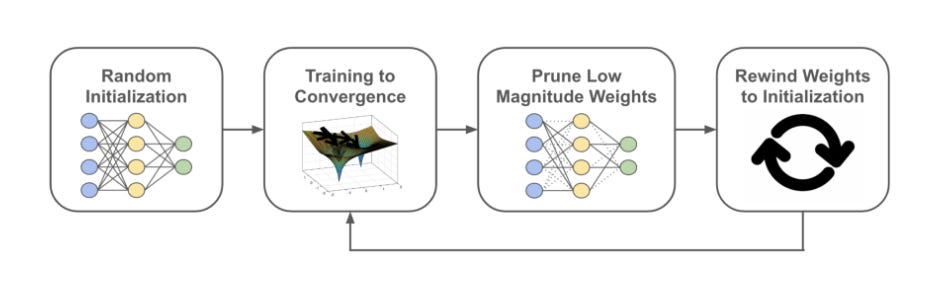
The Four steps to identify the Winning ticket:
1. Randomly initialize a neural network.
2. Train the network for a number of iterations, arriving at parameters at the respected number of iterations.
3. Prune the parameters currently attained, creating a mask.
4. Reset the remaining parameters to their original values, creating the winning ticket we require for retraining the pruned network.
Conditions to be met: Randomly re-initializing winning tickets prior to training is damaging to performance. Hence rewinding parameters to their initial, random values is essential to matching or exceeding dense network performance.
Summary:
Neural network pruning techniques can reduce the parameter counts of trained networks by over 90%, decreasing storage requirements and improving the computational performance of inference without compromising accuracy.
We consistently find winning tickets that are less than 10-20% of the size of several fully-connected and convolutional feed-forward architectures for MNIST and CIFAR10. Above this size, the winning tickets that we find learn faster than the original network and reach higher test accuracy.
Winning tickets are shown to have better generalization properties than the original dense network in many cases.
Conclusion:
It improves training performance and also helps to accelerate the training of neural networks.
There is a massive speed storage improvement.
It helps to design better networks by getting more areas for experimentation.
Improve theoretical understanding of neural networks.
Subscribe to receive a copy of our newsletter directly delivered to your inbox.
The above article is sponsored by Vevesta.
Vevesta: Your Machine Learning Team’s Feature and Technique Dictionary - Accelerate your Machine learning project by using features, techniques and projects used by your peers
100 early birds who login into Vevesta will get free subscription for 3 months




Amazing work.
Very well put