Introducing Model Soups - How to Increase Accuracy of Fine Tuned LLMs Without Increasing Inference Time ?

TLDR - Brief summary of the paper on Model soups: Averaging weights of multiple fine-tuned models improves accuracy without increasing inference time

Photo by Matthew Hamilton on Unsplash

---

I blog about latest machine learning research topics that have an immediate impact on the work us data scientists/machine learning engineers do every day. Share the newsletter with your friends so that we all grow together.

---

Recent research effort has been to improve accuracy of fine-tuned LLMs while reducing training time and cost. This article details how to improve performance specially on out of distribution data without really spending any additional time and cost on training the models.

Need for Model Soup

1. Despite the high computational cost during inference, it has been observed multiple times that ensembling outputs of many models can outperform the best single model.

2. According to authors, “The best single model on the target distribution may not be the best model on out-of-distribution data.”

3. Fine tuning LLMs on downstream tasks can sometime reduce performance on out of distribution data.

What is Model Soup ?

While fine tuning a model on a particular task, number of fine tuned models are generated in the process. The authors propose that averaging weights of independently fine tuned models. This they call as model soup. The advantage of this technique is that there is no additional training required and it doesn’t add additional time to inference. “The insight for this work is drawn from another research paper that observed that fine-tuned models optimized independently from the same pre-trained initialization lie in the same basin of the error landscape”. They also found that model soups often outperform the best individual model on both the in-distribution and natural distribution shift test sets.

Types of Model Soups

There are three types of Model Soups:- Learned Soup, Greedy Soup and Uniform Soup. Let

\(θ = FineTune(θ_{0}, h)\)

denote the parameters obtained by fine-tuning with pre-trained initialization θ0 and hyperparameter configuration h. Model soups f(x, θS ) use an average of θi.

The primary methods contrasted in this work. Each θi is a model found through fine-tuning from a shared initialization. Cost refers to the memory and compute requirements during inference relative to a single model. All methods require the same training.

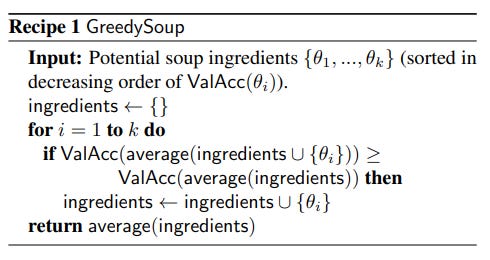
Authors[1] have primarily focused their attention of Greedy Soup. “Greedy soup is constructed by sequentially adding each model as a potential ingredient in the soup, and only keeping the model in the soup if performance on a held out validation set (disjoint from the training and test sets) improves. Before running this procedure we sort the models in decreasing order of validation set accuracy, and so the greedy soup can be no worse than the best individual model on the held-out validation set.”

Performance Comparison

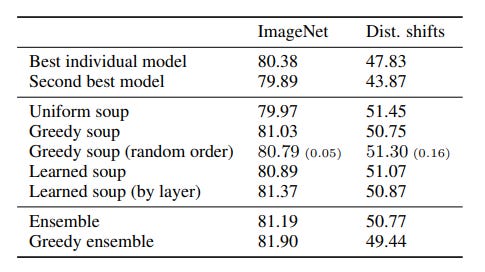
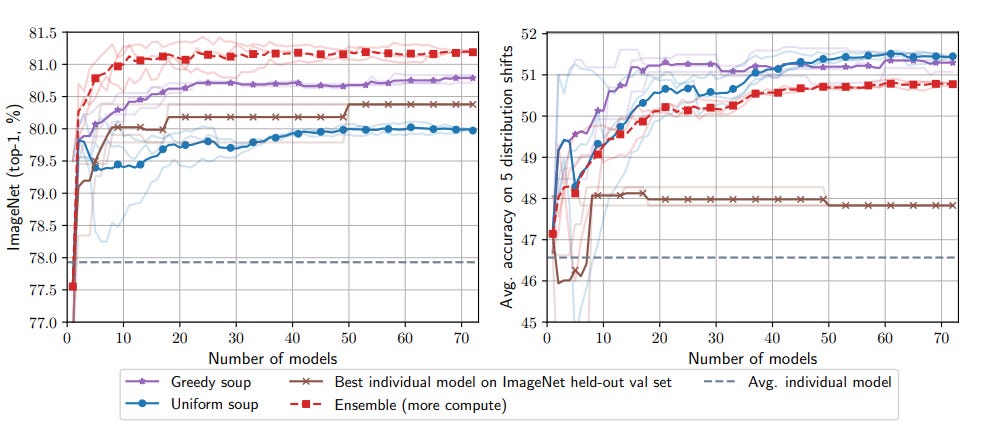
Authors state that “for essentially any number of models, the greedy soup outperforms the best single model on both the ImageNet and the out-of-distribution test sets. The greedy soup is better than the uniform soup on ImageNet and comparable to it out-of-distribution.”

For “Greedy soup (random order)”, authors[1] try three random model orders when running the greedy soup procedure (by default, models are sorted by decreasing held-out val accuracy). The best in best individual model refers to ImageNet accuracy.

For essentially any number of models, the greedy soup outperforms the best single model on both ImageNet and the out-of-distribution test sets. On the x-axis we show the number of models considered in a random search over hyperparameters while the y-axis displays the accuracy of various methods for model selection which are summarized in Table 2. All methods require the same amount of training and compute cost during inference with the exception of the ensembles, which require a separate pass through each model. Results are for fine-tuning CLIP ViT-B/32, averaged over three random orders (shown with faded lines).

Limitations of Model Soups

1. According to authors[1], the performance improvement while using model soups(greedy model soup) is higher for heterogenous models, but one sees marginal improvement when used for models such as ImageNet22k pre-trained model.

2. Model soups don’t improve model calibration, while ensemble models have been shown to improve model calibration.

   

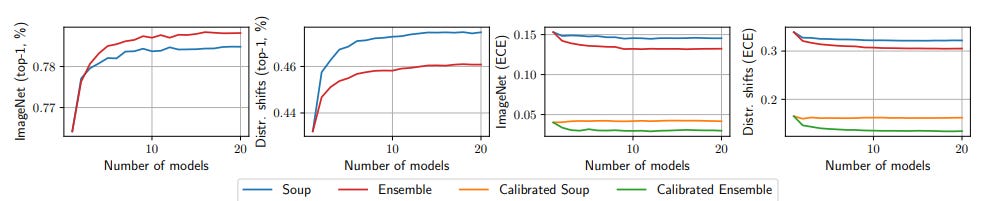
   Like model ensembling, model soups improve accuracy, but unlike model ensembling, model soups do not improve calibration. Expected calibration error (ECE) is computed using equal-mass binning. The soup in this figure is the uniform soup, and all models in this experiment are fine-tuned CLIP ViT-B/32 models with the same hyperparameters but different random seeds. The calibrated soup and calibrated ensemble refer to a soup and ensemble composed of models which are calibrated through temperature scaling (Guo et al., 2017). Calibrating models before ensembling or souping had no effect on accuracy and so these curves are omitted from the plots on the left.

References

1. Original Paper that the article is based on - Model Soups: Averaging weights of multiple fine-tuned models improves accuracy without increasing inference time