Everything you need to know about Activation Functions
The need, the types and the drawbacks of different activation functions
Our human brain learns any objective presented to it with unprecedented speed and accuracy. It has left humankind baffled as to how remarkable our brain is and its ability to learn patterns. Recognition is the core feature in our evolution from savages to intelligent beings. Similarly, activation functions give machines the ability to differ and learn from their output. Although simple to understand, it’s a great feat to make machines capable of mastering many arduous tasks which are difficult for us; human beings.
Before we take a look into activation functions, we must know what a neural network is and what this paradigm consists of.
Introduction to Neural Networks
A Neural Network is a Machine Learning mechanism that potentially mirrors the way a human brain works. To make any impulsive action, a brain gets subjected to countless triggers from the sensors, this load of the received information is processed with the blink of an eye and delivers an output to make a decisive reaction. The more complex the work more neurons take part in the decision-making process and form a complex network, sharing the information within themselves.
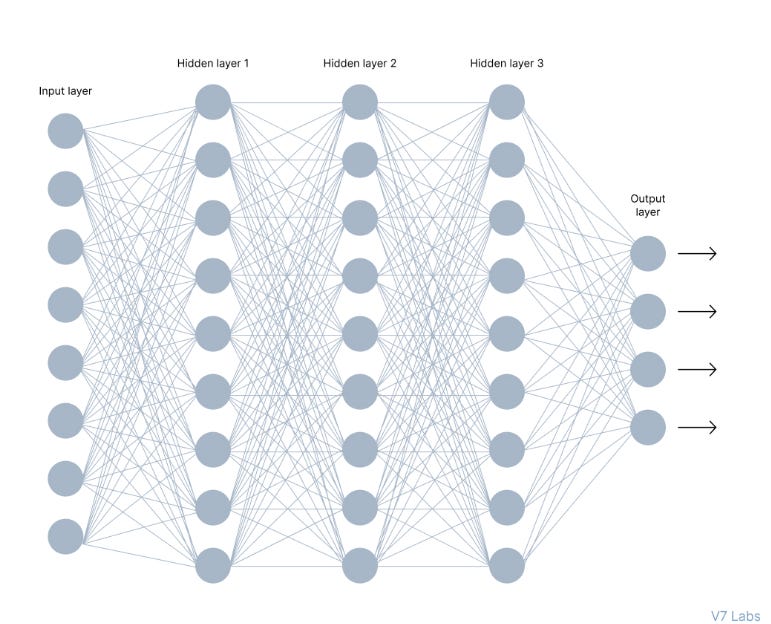
An Artificial Neural Network mimics this behavior to solve problems beyond the capabilities of human computing. The network below is a neural network made of interconnected neurons where each neuron is uniquely distinguished by its weight and bias.
What is an Activation Function?
The Activation function calculates the weighted sum of the inputs accumulating the bias along with it and then makes the decision whether to activate the neuron or not.
The input is fed to the input layer, the neurons perform a linear transformation on this input using the weights and biases.
So we consider a neuron,
The value of Y can be anything ranging from -inf to +inf. Here the neuron doesn’t know the limits of this value, so to take control of this resolution “activation functions” are added to guide the neurons. It governs each neuron in the artificial neural network, to check the Y value produced by a neuron and decide whether this neuron should be enabled or not.
The aftermath from the activation function moves ahead to the hidden layer or another and the same process is repeated. This forward movement of information is known as feed-forward propagation. Which snowballs to the desired result.
However, if the result is far off from what was expected, using the output of the feed-forward propagation, the error is calculated. Depending on this error value, the weights and biases of the neurons are optimized. This process is known as back-propagation.
The need for Activation Functions
The purpose of the activation function is to introduce non-linearity into the output of a neuron. A neural network without activation functions is essentially a linear regression model. Although a linear equation is a polynomial of one degree, which is simple to solve, a neuron can not learn with just a linear function attached. So, the activation function does the non-linear transformation to the inputs concerning the error and gifts the machine an ability to learn.
The choice of activation function in the hidden layer will control how well the network model learns the training dataset. The choice of activation function in the output layer will define the type of predictions the model can make. This ensures that neurons build a network suitable for the given task and the weights are shared accordingly.
Types of Activation Functions
Activation functions are further classified into two types,
Fixed shape activation functions
Trainable activation functions
We must see the activation functions of both these categories to have a clear understanding of how each differs from the other.
Fixed Shape Activation Functions
Being called the “fixed-shape activation functions”, it defines all the activation functions that are deprived of parameters that can be modified during the training phase. All the classic activation functions used in neural network literature, such as sigmoid, tanh, ReLU, fall into this category.
Out of all the functions of this taxonomy, ReLU or Rectified Linear Unit has left the deep learning community as a whole to be in awe and has led the researchers to solve problems that were considered to be an enigma. It has left a significant impact, so much so that it’s considered the rudimentary foundation of deep learning.
To understand the real significance of Relu we have a brief overview of the sigmoid function and the vanishing gradients.
The Vanishing Gradient
The sigmoid function is shaped like the S aphabet as given below. It is non-linear in nature.
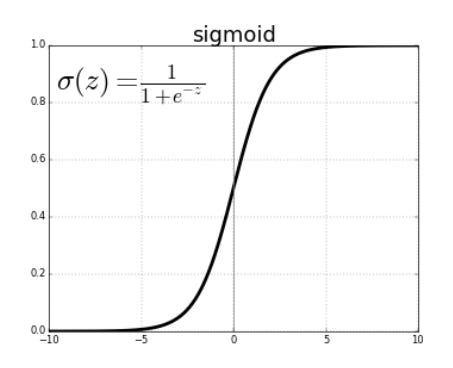
It has a smooth gradient and transforms the values between 0 to 1
The sigmoid function is especially used for models where we have to predict the probability as an output. Since the probability of anything exists only between the range of 0 and 1.
This function has steep Y values to the corresponding X values. This means any changes in the values of X in that region will cause values of Y to change drastically, meaning it tends to bring the Y values to either end of the curve and thus is a good binary classifier.
As the function only trains within the closed range of roughly -6 to 6. the Y values tend to respond very less to changes in X. This is because beyond the limits on either side of the gradients are insignificant. It gives rise to a problem of “vanishing gradients”. Because of this reason, using the sigmoid function in a deep network is not prefered.
ReLU is the first workaround to overcome the undesired outcomes of the sigmoid function.
ReLU
ReLU or Rectified Linear Unit is another non-linear activation function.
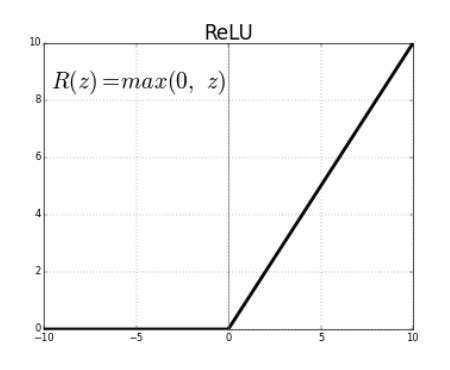
ReLU is simply outputting the non-negative output of a neuron. However, as you might have noted, ReLU simply does not exist in the negative space.
The derivatives are never dead in the positive region. As the values are output as it is without any dampening, values will not vanish as we saw in the sigmoid function.
The main advantage of using the ReLU function over other activation functions is the sparsity of the activation. It does not activate all the neurons at the same time, since for all the negative values the result is zero. Hence is more computationally effective.
The Downfall of ReLU
Since this function has no presence in the negative X direction, the gradient can go towards 0. For activations in that region of ReLu, the gradient will be 0 because of which the weights will get disjointed during descent. The neurons which go into this state will become an empty husk that responds to no stimuli. The neuron never learns and causes almost a sigmoid like saturation. This is called the dying ReLu problem.
Trainable activation functions
This class contains all the activation functions, the shape of which is learned during the training phase. It implies that, unlike the fixed shape activation functions, these functions can morph and fit the function giving it a superior edge over the fixed shape functions. We will thus delve deeper and look at the successor of ReLU known as Parametric ReLU
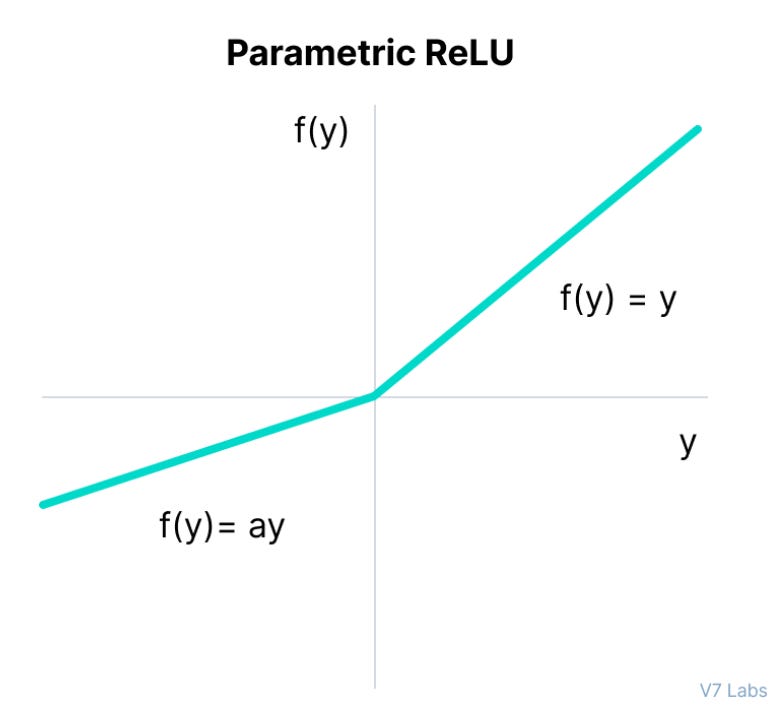
Parametric ReLU
Leaky ReLU, is a variant of a ReLU function, but it has a small slope for negative values instead of a flat slope. The slope coefficient is determined before training, meaning that it is a fixed-shaped activation function and the slope is not learnt during training.
Introducing the ReLU variation function that partially learns its shape from the training set, Parametric ReLU tries to parameterize the negative input thus enabling the recovery of the dying ReLU.
The mathematical function of PReLU is given as follows:
Where "a" is the slope parameter for negative values.
The network also learns the value of a and changes it every training iteration for faster and more optimum convergence.
Since the negative pre-activations produce negative values instead of 0, we do not have the problem regarding weights being updated only in one direction that was associated with ReLU.
This fixes the problem of the dying ReLU problem and enhances the same function by being parameterized and adaptable.
Conclusion
Linear functions evolved to be able to solve intricate problems by the use of Activation functions.
Activation functions administer the firing or avoiding of a neuron, which helps the weights to shift to the neuron which proves better results and also a well-built neural network altogether.
Sigmoid function is exceptional at solving binary classification problems
Activation functions must be chosen by looking at the range of the input values. However, ReLU or PReLU is a good starting point with sigmoid or softmax to the output layer.
The undeniable advantage that the Trainable functions have over the Fixed Shape Functions.
There is still a wide field of research getting conducted on activation functions and how to get them to peak performance by little to no tweaking.
Vevesta: Your Machine Learning Team’s Collective Wiki: Identify and use relevant machine learning projects, features and techniques.
100 early birds who login into Vevesta will get free subscription for 3 months
References
This article was originally published at https://www.vevesta.com/blog/28-Activation-Functions



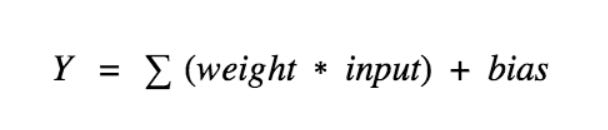
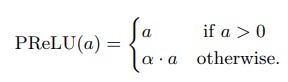
Good going joshua 😊