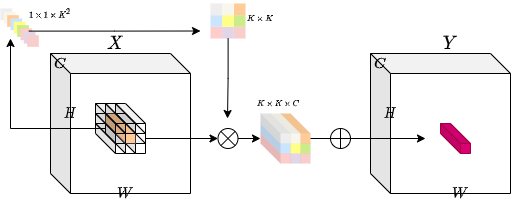Beginner’s Guide to Involutional Neural Networks
How Involutional Neural Networks compare with established CNNs
Starting from the basics, Neural Networks are algorithms created explicitly to simulate biological neural networks. Generally, the idea was to create an artificial system that would function like the human brain. Neural networks are based on interconnected neurons depending on the type of network. There are many types of neural networks, but we will cover significant differences between convolutional neural networks and involutional neural networks.
The word agnostic comes from Greek, a-, meaning without and gnōsis, meaning knowledge. In IT, that translates to the ability of something to function without “knowing” the underlying details of a system that it is working within.
Convolutional Neural Networks (CNN), being spatial-agnostic and channel-specific — the fundamental principle has been the core ingredient of modern neural networks, triggering the surge of deep learning in vision.
But it isn’t able to adapt to different visual patterns with respect to different spatial locations. In layman’s language, CNN finds it difficult to bring out results if the location of the particular visual pattern is changed in space. Along with location-related problems, the receptive field of convolution creates challenges with regard to capturing long-range spatial interactions.
These issues can be solved by inverting the design principles of convolution that could be leveraged as fundamental bricks to build the new generation of neural networks for visual recognition — Involution.
Now, what exactly is Involution?
Involution is location-specific and channel-agnostic. Due to the location-specific nature of the operation, the authors say that self-attention falls under the design paradigm of involution.
We can say that involution is reminiscent of self-attention and essentially could become a generalized version of it.
That means involution provides attention to individual spatial positions of the input tensor. The location-specific property makes involution a generic space of models in which self-attention belongs.
Involution powers different deep learning models on several prevalent benchmarks, including ImageNet classification, COCO detection and segmentation, together with Cityscapes segmentation. The resulting Involution Operator and RedNet architecture are a compromise between classic Convolutions and the newer Local Self-Attention architectures and perform favourably in terms of computation accuracy tradeoff when compared to either. Involution-based models improve the performance of convolutional baselines using ResNet-50 by up to 1.6% top-1 accuracy, 2.5% and 2.4% bounding box AP, and 4.7% mean IoU absolutely while compressing the computational cost to 66%, 65%, 72%, and 57% on the above benchmarks, respectively.
Setup:
import tensorflow as tf
from tensorflow import keras
import matplotlib.pyplot as plt
# Set seed for reproducibility.
tf.random.set_seed(42)class Involution(keras.layers.Layer):
def __init__(
self, channel, group_number, kernel_size, stride, reduction_ratio, name
):
super().__init__(name=name)
# Initialize the parameters.
self.channel = channel
self.group_number = group_number
self.kernel_size = kernel_size
self.stride = stride
self.reduction_ratio = reduction_ratio
def build(self, input_shape):
# Get the shape of the input.
(_, height, width, num_channels) = input_shape
# Scale the height and width with respect to the strides.
height = height // self.stride
width = width // self.stride
# Define a layer that average pools the input tensor
# if stride is more than 1.
self.stride_layer = (
keras.layers.AveragePooling2D(
pool_size=self.stride, strides=self.stride, padding="same"
)
if self.stride > 1
else tf.identity
)
# Define the kernel generation layer.
self.kernel_gen = keras.Sequential(
[
keras.layers.Conv2D(
filters=self.channel // self.reduction_ratio, kernel_size=1
),
keras.layers.BatchNormalization(),
keras.layers.ReLU(),
keras.layers.Conv2D(
filters=self.kernel_size * self.kernel_size * self.group_number,
kernel_size=1,
),
]
)
# Define reshape layers
self.kernel_reshape = keras.layers.Reshape(
target_shape=(
height,
width,
self.kernel_size * self.kernel_size,
1,
self.group_number,
)
)
self.input_patches_reshape = keras.layers.Reshape(
target_shape=(
height,
width,
self.kernel_size * self.kernel_size,
num_channels // self.group_number,
self.group_number,
)
)
self.output_reshape = keras.layers.Reshape(
target_shape=(height, width, num_channels)
)
def call(self, x):
# Generate the kernel with respect to the input tensor.
# B, H, W, K*K*G
kernel_input = self.stride_layer(x)
kernel = self.kernel_gen(kernel_input)
# reshape the kerenl
# B, H, W, K*K, 1, G
kernel = self.kernel_reshape(kernel)
# Extract input patches.
# B, H, W, K*K*C
input_patches = tf.image.extract_patches(
images=x,
sizes=[1, self.kernel_size, self.kernel_size, 1],
strides=[1, self.stride, self.stride, 1],
rates=[1, 1, 1, 1],
padding="SAME",
)
# Reshape the input patches to align with later operations.
# B, H, W, K*K, C//G, G
input_patches = self.input_patches_reshape(input_patches)
# Compute the multiply-add operation of kernels and patches.
# B, H, W, K*K, C//G, G
output = tf.multiply(kernel, input_patches)
# B, H, W, C//G, G
output = tf.reduce_sum(output, axis=3)
# Reshape the output kernel.
# B, H, W, C
output = self.output_reshape(output)
# Return the output tensor and the kernel.
return output, kernelTesting the Involution layer
# Define the input tensor.
input_tensor = tf.random.normal((32, 256, 256, 3))
# Compute involution with stride 1.
output_tensor, _ = Involution(
channel=3, group_number=1, kernel_size=5, stride=1, reduction_ratio=1, name="inv_1"
)(input_tensor)
print(f"with stride 1 ouput shape: {output_tensor.shape}")
# Compute involution with stride 2.
output_tensor, _ = Involution(
channel=3, group_number=1, kernel_size=5, stride=2, reduction_ratio=1, name="inv_2"
)(input_tensor)
print(f"with stride 2 ouput shape: {output_tensor.shape}")
# Compute involution with stride 1, channel 16 and reduction ratio 2.
output_tensor, _ = Involution(
channel=16, group_number=1, kernel_size=5, stride=1, reduction_ratio=2, name="inv_3"
)(input_tensor)
print(
"with channel 16 and reduction ratio 2 ouput shape: {}".format(output_tensor.shape)
)Image Classification
Now that we are done with the testing of involutional layer, the next step is to build an image-classifier model.
There will be two models — one with convolutions and the other with involutions.
The image-classification model is heavily inspired by this Convolutional Neural Network (CNN) tutorial from Google.
Get the CIFAR10 Dataset
# Load the CIFAR10 dataset.
print("loading the CIFAR10 dataset...")
(train_images, train_labels), (
test_images,
test_labels,
) = keras.datasets.cifar10.load_data()
# Normalize pixel values to be between 0 and 1.
(train_images, test_images) = (train_images / 255.0, test_images / 255.0)
# Shuffle and batch the dataset.
train_ds = (
tf.data.Dataset.from_tensor_slices((train_images, train_labels))
.shuffle(256)
.batch(256)
)
test_ds = tf.data.Dataset.from_tensor_slices((test_images, test_labels)).batch(256)Visualise the data
class_names = [
"airplane",
"automobile",
"bird",
"cat",
"deer",
"dog",
"frog",
"horse",
"ship",
"truck",
]
plt.figure(figsize=(10, 10))
for i in range(25):
plt.subplot(5, 5, i + 1)
plt.xticks([])
plt.yticks([])
plt.grid(False)
plt.imshow(train_images[i])
plt.xlabel(class_names[train_labels[i][0]])
plt.show()Convolutional Neural Network
# Build the conv model.
print("building the convolution model...")
conv_model = keras.Sequential(
[
keras.layers.Conv2D(32, (3, 3), input_shape=(32, 32, 3), padding="same"),
keras.layers.ReLU(name="relu1"),
keras.layers.MaxPooling2D((2, 2)),
keras.layers.Conv2D(64, (3, 3), padding="same"),
keras.layers.ReLU(name="relu2"),
keras.layers.MaxPooling2D((2, 2)),
keras.layers.Conv2D(64, (3, 3), padding="same"),
keras.layers.ReLU(name="relu3"),
keras.layers.Flatten(),
keras.layers.Dense(64, activation="relu"),
keras.layers.Dense(10),
]
)
# Compile the mode with the necessary loss function and optimizer.
print("compiling the convolution model...")
conv_model.compile(
optimizer="adam",
loss=keras.losses.SparseCategoricalCrossentropy(from_logits=True),
metrics=["accuracy"],
)
# Train the model.
print("conv model training...")
conv_hist = conv_model.fit(train_ds, epochs=20, validation_data=test_ds)Involutional Neural Network
# Build the involution model.
print("building the involution model...")
inputs = keras.Input(shape=(32, 32, 3))
x, _ = Involution(
channel=3, group_number=1, kernel_size=3, stride=1, reduction_ratio=2, name="inv_1"
)(inputs)
x = keras.layers.ReLU()(x)
x = keras.layers.MaxPooling2D((2, 2))(x)
x, _ = Involution(
channel=3, group_number=1, kernel_size=3, stride=1, reduction_ratio=2, name="inv_2"
)(x)
x = keras.layers.ReLU()(x)
x = keras.layers.MaxPooling2D((2, 2))(x)
x, _ = Involution(
channel=3, group_number=1, kernel_size=3, stride=1, reduction_ratio=2, name="inv_3"
)(x)
x = keras.layers.ReLU()(x)
x = keras.layers.Flatten()(x)
x = keras.layers.Dense(64, activation="relu")(x)
outputs = keras.layers.Dense(10)(x)
inv_model = keras.Model(inputs=[inputs], outputs=[outputs], name="inv_model")
# Compile the mode with the necessary loss function and optimizer.
print("compiling the involution model...")
inv_model.compile(
optimizer="adam",
loss=keras.losses.SparseCategoricalCrossentropy(from_logits=True),
metrics=["accuracy"],
)
# train the model
print("inv model training...")
inv_hist = inv_model.fit(train_ds, epochs=20, validation_data=test_ds)Comparisons
Now, we will compare the models on the basis of:
Parameters
Loss and Accuracy Plots
1. Parameters:
We can see that with a similar architecture, the parameters in a CNN (Convolutional Neural Network) is much larger than that of an INN (Involutional Neural Network).
conv_model.summary()inv_model.summary()2. Loss and Accuracy Plots:
Here, the loss and the accuracy plots demonstrate that INNs are slow learners since they have lower parameters as compared to CNNs.
plt.figure(figsize=(20, 5))plt.subplot(1, 2, 1)
plt.title("Convolution Loss")
plt.plot(conv_hist.history["loss"], label="loss")
plt.plot(conv_hist.history["val_loss"], label="val_loss")
plt.legend()plt.subplot(1, 2, 2)
plt.title("Involution Loss")
plt.plot(inv_hist.history["loss"], label="loss")
plt.plot(inv_hist.history["val_loss"], label="val_loss")
plt.legend()plt.show()plt.figure(figsize=(20, 5))plt.subplot(1, 2, 1)
plt.title("Convolution Accuracy")
plt.plot(conv_hist.history["accuracy"], label="accuracy")
plt.plot(conv_hist.history["val_accuracy"], label="val_accuracy")
plt.legend()plt.subplot(1, 2, 2)
plt.title("Involution Accuracy")
plt.plot(inv_hist.history["accuracy"], label="accuracy")
plt.plot(inv_hist.history["val_accuracy"], label="val_accuracy")
plt.legend()plt.show()Visualizing Involution Kernels
To visualize the kernels, we take the sum of K×K values from each involution kernel. All the representatives at different spatial locations frame the corresponding heat map.
The authors mention:
“Our proposed involution is reminiscent of self-attention and essentially could become a generalized version of it.”
With the visualization of the kernel we can indeed obtain an attention map of the image. The learned involution kernels provides attention to individual spatial positions of the input tensor. The location-specific property makes involution a generic space of models in which self-attention belongs.
layer_names = ["inv_1", "inv_2", "inv_3"]
outputs = [inv_model.get_layer(name).output for name in layer_names]
vis_model = keras.Model(inv_model.input, outputs)
fig, axes = plt.subplots(nrows=10, ncols=4, figsize=(10, 30))
for ax, test_image in zip(axes, test_images[:10]):
(inv1_out, inv2_out, inv3_out) = vis_model.predict(test_image[None, ...])
_, inv1_kernel = inv1_out
_, inv2_kernel = inv2_out
_, inv3_kernel = inv3_out
inv1_kernel = tf.reduce_sum(inv1_kernel, axis=[-1, -2, -3])
inv2_kernel = tf.reduce_sum(inv2_kernel, axis=[-1, -2, -3])
inv3_kernel = tf.reduce_sum(inv3_kernel, axis=[-1, -2, -3])
ax[0].imshow(keras.preprocessing.image.array_to_img(test_image))
ax[0].set_title("Input Image")
ax[1].imshow(keras.preprocessing.image.array_to_img(inv1_kernel[0, ..., None]))
ax[1].set_title("Involution Kernel 1")
ax[2].imshow(keras.preprocessing.image.array_to_img(inv2_kernel[0, ..., None]))
ax[2].set_title("Involution Kernel 2")
ax[3].imshow(keras.preprocessing.image.array_to_img(inv3_kernel[0, ..., None]))
ax[3].set_title("Involution Kernel 3")All in all, this article can be summarized as:
Conclusion:
In this article, the main focus was to build an Involution layer which can be easily reused. While our comparisons were based on a specific task, feel free to use the layer for different tasks and report your results. According to me, the key take-away of involution is its relationship with self-attention. The intuition behind location-specific and channel-specific processing makes sense in a lot of tasks.
Credits:
The above article is sponsored by Vevesta.
Vevesta: Your Machine Learning Team’s Collective Wiki: Identify and use relevant machine learning projects, features and techniques.
100 early birds who login into Vevesta will get free subscription for 3 months
Subscribe to receive a copy of our newsletter directly delivered to your inbox.